Problems
Here you will find detailed information about the problems addressed in iMOPSE.
Multi-Skill Resource-Constrained Project Scheduling Problem (MSRCPSP)
In the Multi-Skill Resource-Constrained Project Scheduling Problem (MSRCPSP), the objective is to create a project schedule that minimizes cost and/or duration. The problem involves scheduling tasks that require specific skills while respecting resource constraints and precedence relations between tasks.
MSRCPSP is represented in two distinct ways within iMOPSE:
- MSRCPSP_TA (Task-Resource Association Encoding): This encoding uses a float vector where each element represents a resource identifier assigned to a corresponding task. This vector specifies the resource each task should use.
- MSRCPSP_TO (Task Order Encoding): This encoding uses an integer permutation vector where each element represents a task identifier. This vector specifies the order in which tasks should be scheduled.
A greedy schedule builder interprets these encodings to construct valid schedules. For the task-resource association encoding (TA), the builder assigns resources directly from the vector. For the task order encoding (TO), it schedules tasks based on their order in the vector and assigns resources to minimize delays.
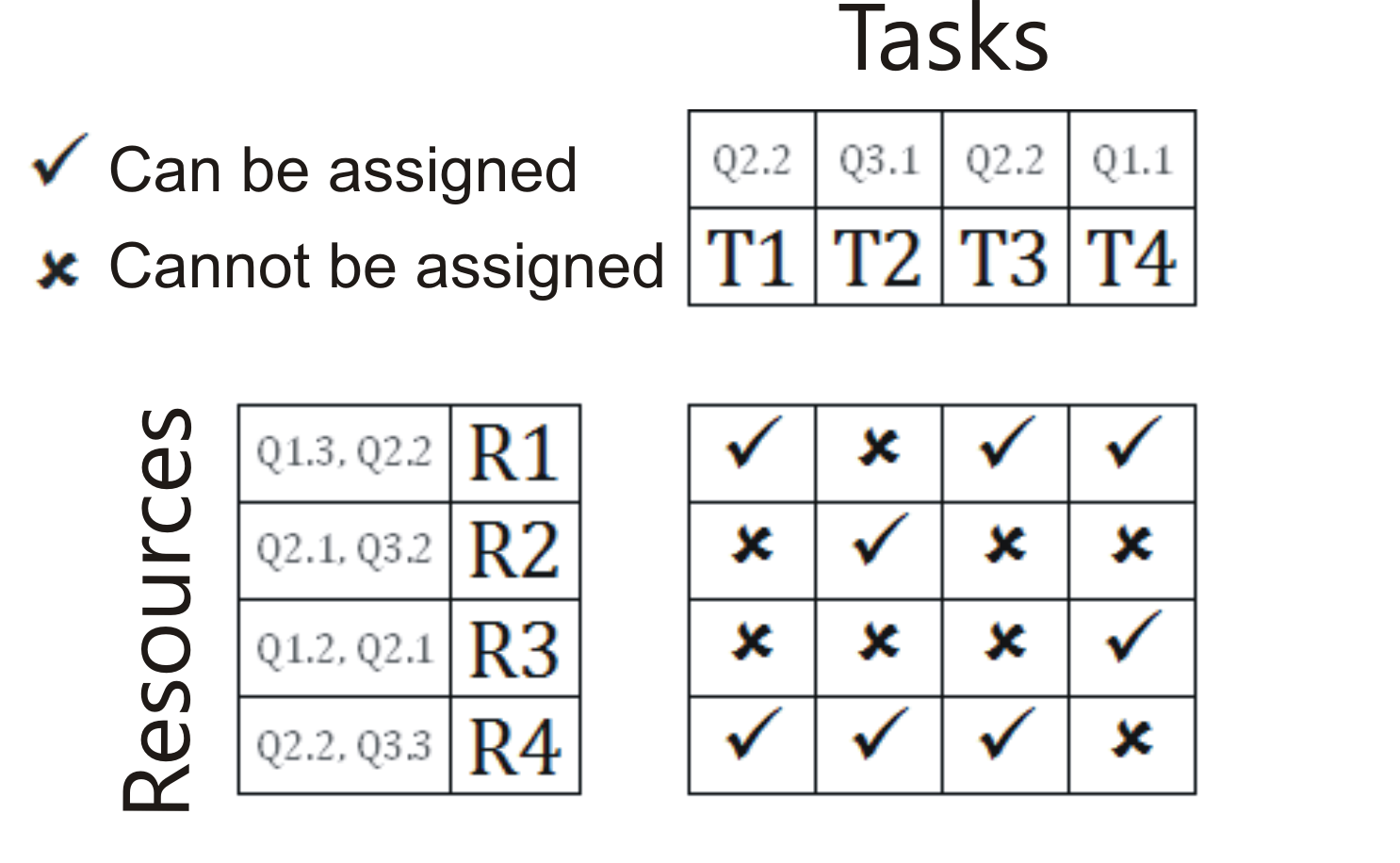
Tasks can be performed by capable resources. A capable resource is one that has a specified skill type with the familiarity level no lower than required by a given task. This means that each task is also described by the skill required to perform it, and if a resource does not possess that specified skill, it cannot be assigned to the task.
The MS-RCPSP problem is similar to the Software Project Scheduling Problem. The proposed MS-RCPSP problem statement differs slightly from the classical RCPSP found in the literature:
- Cost Aspect: Transformation to a multi-criteria optimization problem by adding the cost aspect.
- Task Predecessors: Not every task is required to have predecessors. No dummy finish and start tasks are introduced.
- Resource Description: Resources are not described by units used to define what part of the resource’s time is spent on a given task. In our model, a resource can be assigned to only one task at a given time.
- Conflict Resolution: Assigning more than one task to a given resource in overlapping periods causes conflicts. These conflicts must be resolved by shifting one of the conflicted tasks' start times to just after the finish time of another conflicted task.
- Skills Domain: Introducing the skills domain makes our approach closer to real-world applications in project management.

Moreover, the problem can be considered a multi-criteria optimization problem, focusing on (1) schedule duration optimization and (2) schedule cost realization. To facilitate comparison with other scientific work, we have developed and published benchmark dataset instances, tools (validator, visualizer), and Java library.
The problem can be considered as:
- MSRCPSP_TA: Using task-resource association encoding with one objective (e.g., cost or duration).
- MSRCPSP_TO: Using task order encoding with one objective.
- MSRCPSP_TA2: Using task-resource association encoding with two objectives (e.g., cost and duration).
- MSRCPSP_TO2: Using task order encoding with two objectives.
Travelling Thief Problem (TTP)
The Travelling Thief Problem (TTP) is a combinatorial optimization problem that integrates the Traveling Salesman Problem (TSP) and the Knapsack Problem. The goal is to find a route for a thief that maximizes the total value of items collected while minimizing travel costs and adhering to a knapsack weight limit.
In TTP, the thief must decide the order of cities to visit and which items to pick up at each city. This problem is challenging due to the interplay between the traveling route and the items collected. The encoding for TTP consists of two parts:
- Permutation Encoding (Travel Route): A permutation of cities representing the order in which the thief visits them. This is a sequence where each city is visited exactly once.
- Binary Encoding (Item Collection): A binary vector where each element indicates whether a corresponding item is collected (1) or not (0) at a city.
The thief's objective is to maximize the total profit, which is the total value of collected items minus the travel cost. This involves balancing the trade-off between collecting valuable items and the additional travel costs incurred.
- TTP1: Single objective TTP, focusing solely on profit maximization.
- TTP2: Multi-objective TTP, considering both profit maximization and travel cost minimization.
Travelling Salesman Problem (TSP)
The Travelling Salesman Problem (TSP) is a classic combinatorial optimization problem. The objective is to determine the shortest possible route that visits a set of cities exactly once and returns to the starting city.
In TSP, the encoding is represented using permutation encoding, where each element in the permutation represents a city. This encoding allows the algorithm to explore different sequences of city visits.
The challenge in TSP lies in finding the shortest possible route, which becomes increasingly difficult as the number of cities grows. TSP is widely used to test and benchmark optimization algorithms due to its NP-hard nature.
- TSP: Single objective TSP focusing on minimizing the total travel distance. This problem is crucial in fields such as logistics, manufacturing, and DNA sequencing.
Capacitated Vehicle Routing Problem (CVRP)
The Capacitated Vehicle Routing Problem (CVRP) involves determining the optimal set of routes for a fleet of vehicles to deliver goods to customers with known demands. The objective is to minimize the total travel distance while considering vehicle capacity constraints.
In CVRP, the problem is represented using permutation encoding. Each permutation represents a route for a vehicle, and the objective is to determine the best set of routes that minimizes the total distance traveled.
CVRP is challenging because it not only requires finding the shortest routes but also ensuring that the routes respect the capacity constraints of each vehicle. This makes CVRP a valuable problem for testing and benchmarking optimization algorithms in the logistics and transportation industries.
- CVRP: Single objective CVRP focusing on minimizing the travel distance while respecting the capacity constraints of each vehicle. Efficient solutions to CVRP can lead to significant cost savings in transportation and logistics operations.